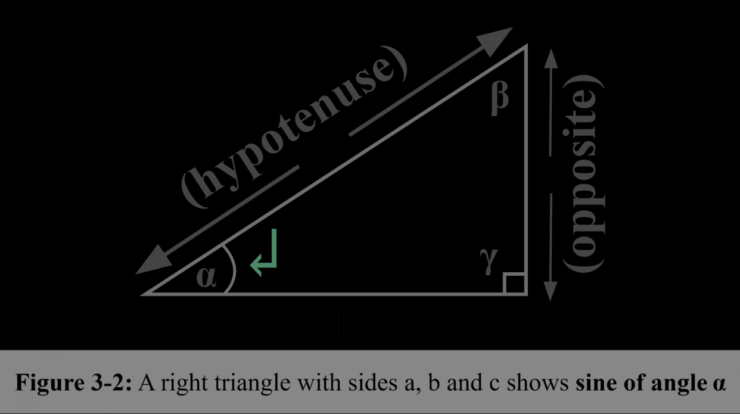
Sine meaning delves into the intriguing world of trigonometry, exploring the mathematical essence of sine as a function that defines the vertical component of a right triangle. Its applications extend far beyond the classroom, with sine playing a pivotal role in fields like physics, engineering, and signal processing.

From its humble beginnings in ancient civilizations to its modern-day significance, the sine function has captivated mathematicians and scientists alike. Its properties, periodicity, and versatility make it an indispensable tool for understanding the complexities of our physical world.

Definitions of Sine

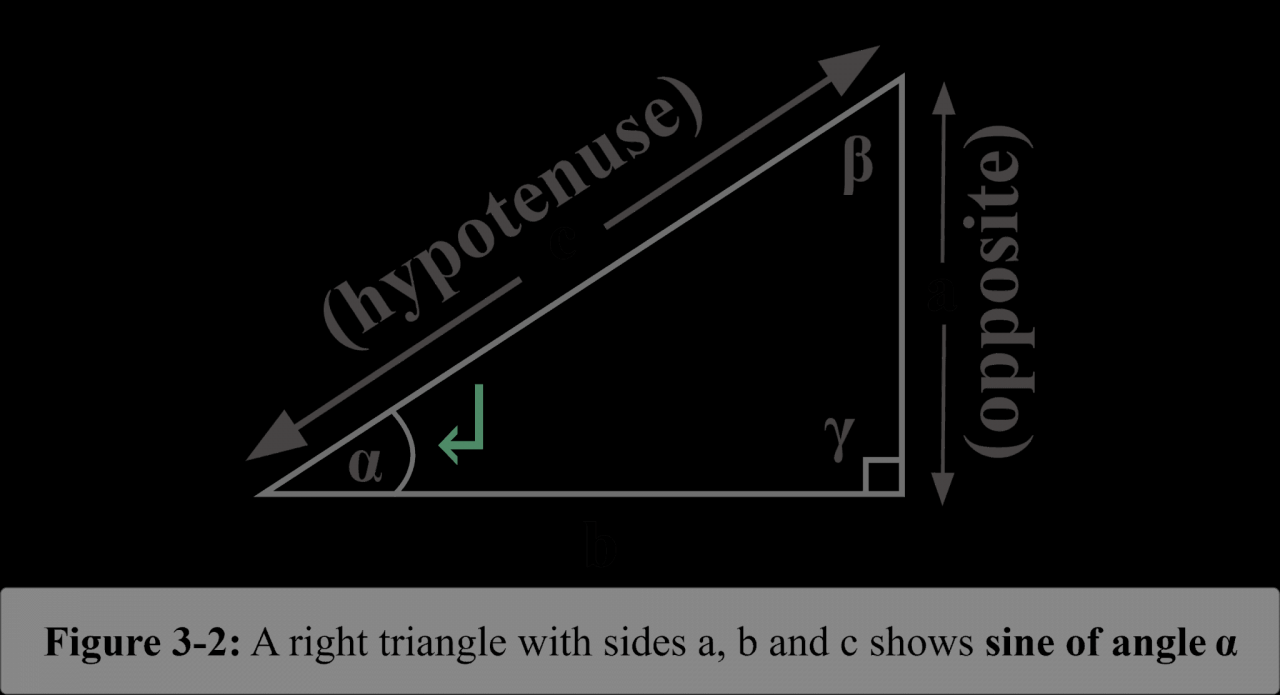
Sine is a trigonometric function that describes the vertical component of a point moving along a unit circle. Mathematically, it is defined as the ratio of the length of the opposite side to the length of the hypotenuse of a right triangle.

Sine finds applications in various fields, such as physics, engineering, and sound waves. In physics, sine is used to describe the motion of objects in periodic motion, such as the oscillation of a pendulum or the vibration of a string.

In engineering, sine is used to analyze the behavior of structures under dynamic loads, such as wind or earthquakes.

Properties of Sine

Sine is a periodic function with a period of 2π. This means that the sine function repeats itself every 2π units. The amplitude of a sine function is the maximum value of the function, and the period is the distance between two consecutive peaks or troughs of the function.

The phase shift of a sine function is the horizontal displacement of the function from its original position. A positive phase shift moves the function to the left, and a negative phase shift moves the function to the right.

Applications of Sine

Sine is used in sound waves and acoustics to describe the shape of the wave. The amplitude of a sound wave is related to the loudness of the sound, and the frequency of the sound wave is related to the pitch of the sound.

Sine is also used in signal processing and telecommunications to transmit and receive information. Sine waves are used as carrier waves for transmitting data, and the amplitude and frequency of the sine wave can be modulated to encode the information.

Historical Context of Sine, Sine meaning

The concept of sine has been known since ancient times. The first known use of sine was by the Babylonian astronomers around 1900 BC. The Babylonians used sine to calculate the length of the day and the position of the sun.

The Greek mathematician Hipparchus (190-120 BC) developed the first trigonometric table, which included the values of sine for different angles. Ptolemy (90-168 AD) expanded on Hipparchus’ work and wrote a treatise on trigonometry that included a table of sines for every degree.

Sine in Calculus

The derivative of the sine function is the cosine function. The integral of the sine function is the negative cosine function.

Sine is used in calculus to study limits, continuity, and differentiability. Sine is also used in the study of Fourier series, which are used to represent periodic functions as a sum of sine and cosine functions.

Epilogue: Sine Meaning

In conclusion, sine meaning encompasses a rich tapestry of mathematical concepts and practical applications. Its ability to describe periodic phenomena, from sound waves to telecommunication signals, underscores its fundamental importance in our technological age. Understanding sine meaning unlocks a gateway to a deeper appreciation of the intricate workings of the universe.

FAQ Guide

What is the mathematical definition of sine?

Sine is defined as the ratio of the length of the opposite side to the length of the hypotenuse in a right triangle.

How is sine used in physics?

Sine is used to describe periodic motion, such as the oscillation of a pendulum or the vibration of a spring.

What is the significance of the unit circle in understanding sine?

The unit circle is a graphical representation of the sine function, showing how its values vary over a complete cycle.